FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar

7. Deltafunktioner

Kan vi approximera \( \vnabla \cdot \vec{F} = \rho (\vec{r}) \), där laddningsfördelningen motsvarar en punktkälla, på något sätt? T.ex. $$ \begin{equation} \rho_\varepsilon (\vec{r}) = \left\{ \begin{array}{ll} c & r < \varepsilon \\ 0 & r > \varepsilon \end{array} \right. \label{_auto4} \end{equation} $$ Dvs, en "utsmetad" punktladdning där vi väljer \( c \) så att den totala laddningen är \( q \), dvs $$ \begin{equation} \rho_\varepsilon (\vec{r}) = \left\{ \begin{array}{ll} \frac{q}{4\pi\varepsilon^3/3} & r \le \varepsilon \\ 0 & r > \varepsilon \end{array} \right. \label{_auto5} \end{equation} $$

• Vad blir funktionen då \( \varepsilon \to 0^+ \)?
• Det kan vi tyvärr inte definiera.
• \( \rho(\vec{r}) = \lim_{\varepsilon \to 0^+} \rho_\varepsilon(\vec{r}) \) är inte en funktion; sekvensen av funktioner som erhålls genom att variera \( \varepsilon \) kallas för en distribution.

Deltafunktioner i en dimension

Punktkälla i \( D=1 \)

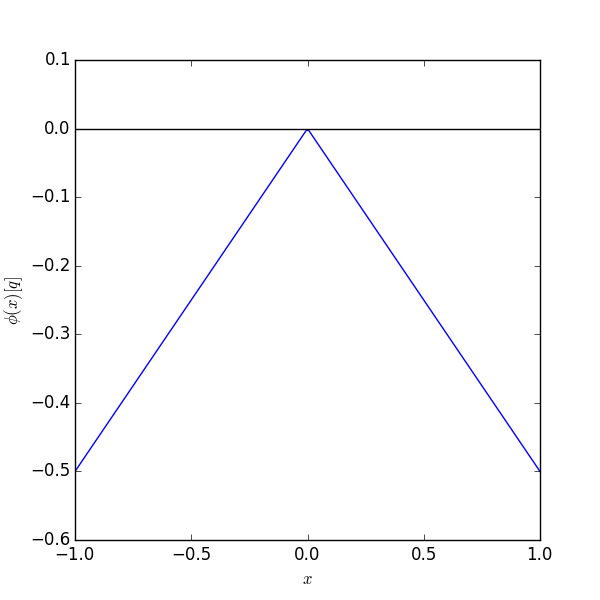
vilket ger fältet $$ \begin{equation} \vec{F}(x) = -\hat{x} \frac{\mbox{d}\phi}{\mbox{d}x} = \left\{ \begin{array}{ll} \frac{q}{2} \hat{x} & x > 0 \\ -\frac{q}{2} \hat{x} & x < 0 \\ \end{array} \right. \label{_auto7} \end{equation} $$

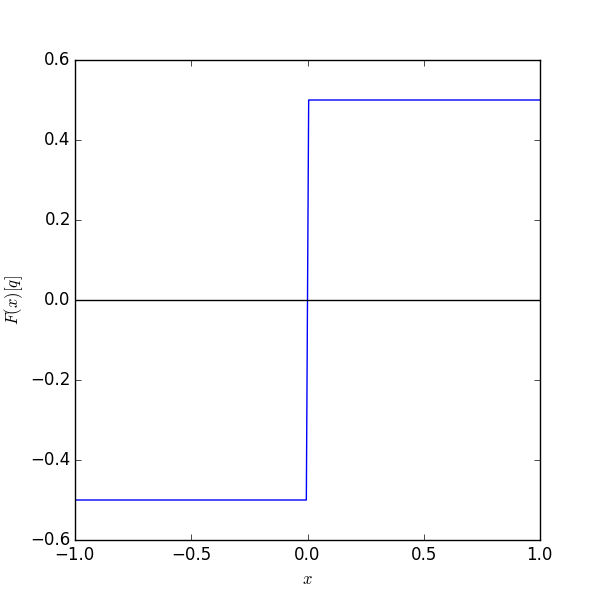
Vi kallar den enda komponenten av detta vektorfält för \( F(x) \), dvs \( F(x) = \frac{q}{2}\sign(x) \). Motsvarigheten till Gauss sats för detta endimensionella fält är $$ \begin{equation} \int_a^b \frac{dF}{dx} dx = F(b) - F(a) = \left\{ \begin{array}{ll} q, & \mathrm{om~} a < 0 < b \\ 0, & \mathrm{annars} \\ \end{array} \right. \label{_auto8} \end{equation} $$ medan en naiv insättning av \( \mbox{d}F / \mbox{d}x = 0 \) i VL hade gett noll.

Problemet är ju att \( \frac{dF}{dx} = 0 \) för \( x \neq 0 \), men "$\frac{dF}{dx} = \infty$" för \( x = 0 \). Vi kan uttrycka detta som en "funktion", \( \frac{dF}{dx} = q \delta(x) \), där

• \( \delta(x) \) är noll då \( x \neq 0 \), och
• integralen \( \int_{a < 0}^{b>0} \delta(x) \mbox{d}x = 1 \).

Distributioner

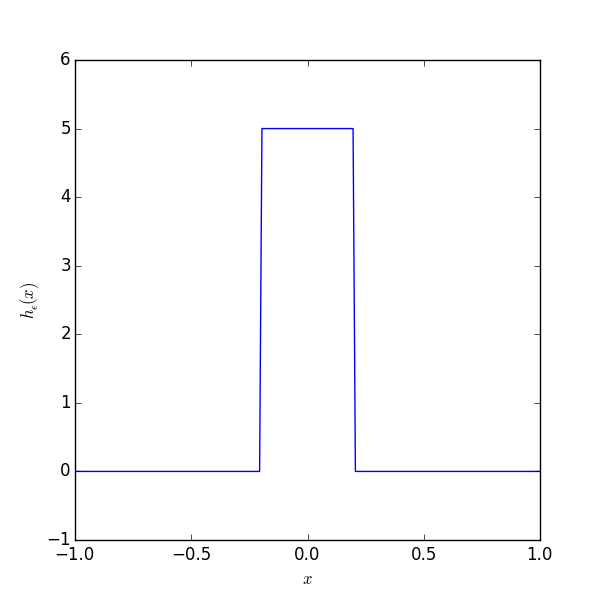
Kontrollera

Men det finns också andra möjligheter: $$ \begin{align} h_\varepsilon(x) &= \frac{\exp(-x^2 / \varepsilon^2)}{\sqrt{\pi} \varepsilon}, \label{_auto10}\\ h_\varepsilon(x) &= \frac{\varepsilon}{\pi (x^2 + \varepsilon^2)}, \label{_auto11}\\ h_\varepsilon(x) &= \frac{\sin(x/\varepsilon)}{\pi x} \label{eq:sinxdelta}. \end{align} $$

import numpy as np
import pylab as p

# Delta function approximation 1 - 4
def h(eps,x,case):
    if case==0:
        h = np.zeros(len(x))
        h [abs(x) < eps] = 1/eps
        return h
    elif case==1:
        return np.exp(-x**2/eps**2) / (np.sqrt(np.pi)*eps)
    elif case==2:
        return eps / (np.pi * (x**2 + eps**2))
    elif case==3:
        return np.sin(x/eps) / (np.sqrt(np.pi)*x)
    
# End initialization

# Start plot
x=np.linspace(-1,1,200)
for case in range(4):
    p.figure(figsize=(6,6))
    for eps in np.linspace(0.5,0.1,5):
        p.plot(x,h(eps,x,case))
    p.xlabel(r'$x$')
    p.ylabel(r'$h_{%i,\epsilon}(x)$' %case)

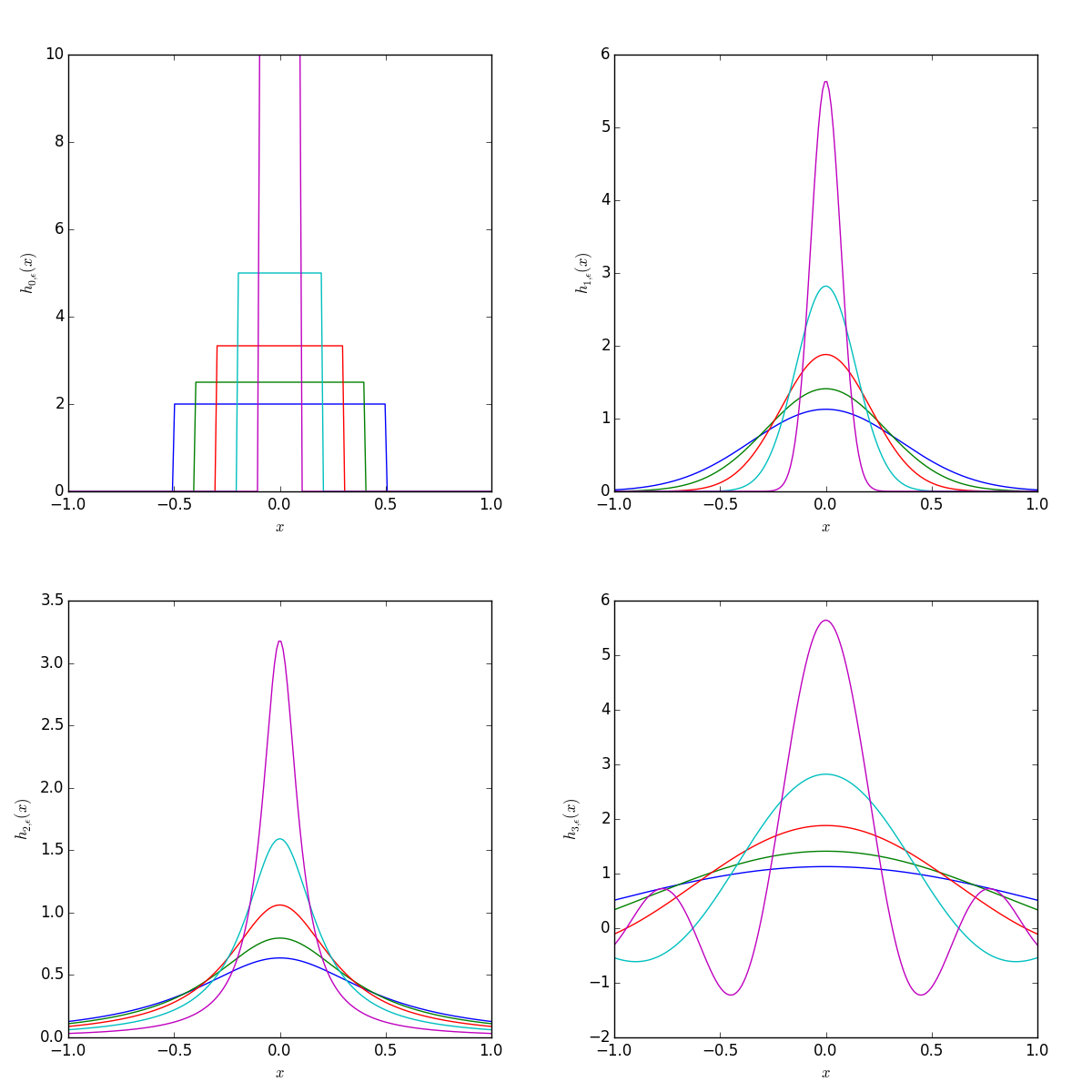
Samtliga dessa utgör en sekvens av funktioner (en distribution) från vilka vi kan definiera Diracs deltafunktion $$ \begin{equation} \delta(x) = \lim_{\varepsilon \to 0^+} h_\varepsilon(x) \label{_auto12} \end{equation} $$ med de definierande egenskaperna

Ett specialfall (\( f(x)=1 \)) av ovanstående är $$ \begin{equation} \int_{-\infty}^{+\infty} \delta(x) \mbox{d}x = 1 \label{_auto15} \end{equation} $$

Egenskaper hos Diracs deltafunktion

• Jämn: $$\delta(-x) = \delta(x)$$
• Skalning:

• Translation:

• Derivata

• Kan generaliseras till fler dimensioner. Vi skriver generellt \( \delta^{(D)}(\vec{r}) \), där vi skall tolka superskriptet som antalet dimensioner. T.ex. har vi för \( D=3 \)

Deltafunktioner i högre dimensioner

Vi startar med punktkällan i origo: \( \vec{F} = \frac{q}{4 \pi r^2} \hat{e}_r \), och den problematiska volymsintegralen $$ \int_V \vnabla \cdot \vec{F} \mbox{d}V, $$ som borde bli lika med \( q \) om \( V \) omfattar origo. Detta kan vi åstadkomma genom att införa \( \vnabla \cdot \vec{F} = q \delta^{(3)}(\vec{r}) = q \delta^{(3)}(x,y,z) \) eftersom $$ \int_V \delta^{(3)}(x,y,z) \mbox{d}x \mbox{d}y \mbox{d}z = 1. $$ Låt oss använda sfäriska koordinater. Hur kan vi uttrycka \( \delta^{(3)}(\vec{r}) \) så att följande integralegenskap uppfylls? $$ \int_V \delta^{(3)}(\vec{r}) r^2 \sin\theta dr d\theta d\varphi = 1, $$ om volymen \( V \) innesluter origo. Vi vill finna \( \delta^{(3)}(\vec{r}) \) som ett gränsvärde av en distribution \( h_\varepsilon(\vec{r}) \).

Starta från ett regulariserat fält $$ \begin{equation} \vec{F}_\varepsilon(\vec{r}) = \frac{q}{4 \pi (r^2 + \varepsilon^2)} \hat{e}_r \label{_auto20} \end{equation} $$ som uppenbarligen går mot \( \vec{F} \) då \( \varepsilon \to 0^+ \).

Divergensen för \( r \neq 0 \) blir (\( \vnabla \cdot \vec{F} = \frac{1}{r^2} \frac{\partial}{\partial r} (r^2 F_r) + \ldots \)) $$ \begin{equation} \vnabla \cdot \vec{F}_\varepsilon(\vec{r}) = \frac{q}{4 \pi r^2} \underbrace{\frac{\partial}{\partial r} \left( \frac{r^2}{r^2 + \varepsilon^2} \right)}_{=\frac{2r}{r^2 + \varepsilon^2} - \frac{2 r r^2}{(r^2 + \varepsilon^2)^2} = \frac{2 r \varepsilon^2}{(r^2 + \varepsilon^2)^2}} = \frac{q \varepsilon^2}{2 \pi} \frac{1}{r(r^2 + \varepsilon^2)^2} \to 0 \quad \mathrm{då} \; \varepsilon \to 0. \label{_auto21} \end{equation} $$ Utan styrkan \( q \) kallar vi denna sekvens av funktioner för \( h_\varepsilon(\vec{r}) \) och påstår att \( \lim_{\varepsilon \to 0} h_\varepsilon(\vec{r}) = \delta^3(\vec{r}) \). Utför integralen $$ \begin{align} \int_V \vnabla \cdot \vec{F}_\varepsilon \mbox{d} V &= \int_V q h_\varepsilon(\vec{r}) \mbox{d} V = \frac{ q \varepsilon^2}{2 \pi} 4\pi \int_0^\infty r^2 \mbox{d} r \frac{1}{r(r^2 + \varepsilon^2)^2} \label{_auto22}\\ &= 2 q \varepsilon^2 \left[ -\frac{1}{2} \frac{1}{r^2 + \varepsilon^2} \right]_0^\infty = 2 q \varepsilon^2 \frac{1}{2 \varepsilon^2} = q \label{_auto23} \end{align} $$ Alltså har vi visat att

• \( \lim_{\varepsilon \to 0} h_\varepsilon(\vec{r}) = 0 \) för \( r \neq 0 \).
• \( \int_{\mathbf{R}^3} h_\varepsilon(\vec{r}) \mbox{d}V = 1 \)

Ett differentiellt uttryck för deltafunktionen $$ \delta^{(3)} \left( \vec{r} \right) = \frac{1}{4\pi} \vec{\nabla} \cdot \frac{\hat{r}}{r^2}, $$ eller mer allmänt $$ \delta^{(3)} \left( \vec{r} - \vec{r}\,' \right) = \frac{1}{4\pi} \vec{\nabla} \cdot \frac{ \left| \vec{r} - \vec{r}\,' \right|}{\left( \vec{r} - \vec{r}\,' \right)^3 }, $$ där vi noterar att \( \vec{\nabla} \) opererar på koordinaten \( \vec{r} \).

Linjekälla

Virveltråd